Δείκτες (Indicators) - Υποενότητα 1
Στην ενότητα των δεικτών (Indicators) περιγράφονται αναλυτικά όλοι οι δείκτες που χρησιμοποιούνται στην τεχνική ανάλυση. Στην υποενότητα 1 αναλύονται οι κινητοί μέσοι όροι.
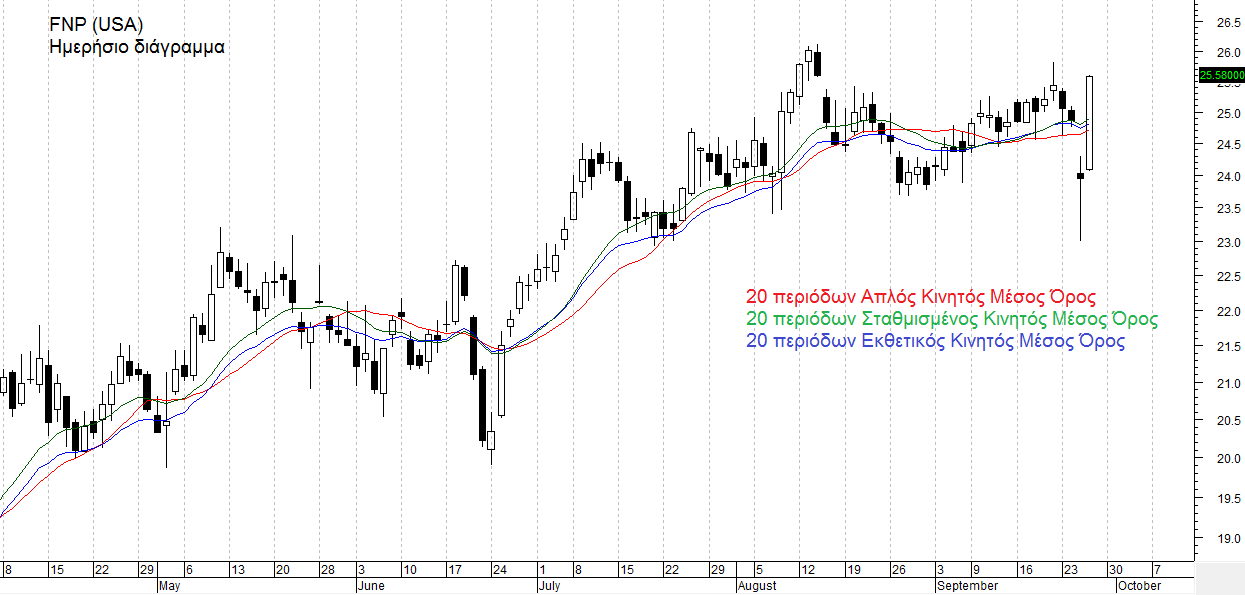
Κινητοί Μέσοι Όροι
Οι κινητοί μέσοι όροι αποτελούν ένα από τα παλαιότερα εργαλεία της Τεχνικής Ανάλυσης και είναι μια δημοφιλής μέθοδος αναγνώρισης και αξιοποίησης των τάσεων.
Χρησιμοποιούνται για:
- να περιορίσουν τις μικρές και μη σημαντικές διακυμάνσεις στην τιμή.
- να βοηθούν στον προσδιορισμό της επικρατούσας τάσης.
Είδη
- Απλός Κινητός Μέσος Όρος (Simple Moving Average)
- Σταθμισμένος Κινητός Μέσος Όρος (Linearly Weighted Moving Average)
- Εκθετικός Κινητός Μέσος Όρος (Exponentially Smoothed Moving Average)
Απλός Κινητός Μέσος Όρος - Περιγραφή
Είναι ο πιο απλός και ευρέως διαδεδομένος κινητός μέσος όρος.
Θα πρέπει να έχουμε υπόψιν ότι η τιμή που προστίθεται και αυτή που αφαιρείται κάθε φορά, μπορούν να επηρεάσουν σημαντικά τον μέσο όρο και ότι όλα τα δεδομένα έχουν την ίδια βαρύτητα.
Ο υπολογισμός ενός n περιόδων SMA γίνεται ως ακολούθως: προσθέτουμε τις τιμές κλεισίματος (δεν είναι κανόνας) των προηγούμενων n περιόδων και διαιρούμε με το n.
Απλός Κινητός Μέσος Όρος - Υπολογισμός
Έστω ότι μου δίνονται οι τιμές κλεισίματος των τελευταίων 6 ημερών:

Για να υπολογίσω τον αριθμητικό μέσο όρο των τελευταίων 6 ημερών προσθέτω τις τιμές κλεισίματος, δηλαδή 5+3+2+4+7+9 και το αποτέλεσμα το διαιρώ με το πλήθος των ημερών (στο συγκεκριμένο παράδειγμα 6).
Άρα: (5+3+2+4+7+9) / 6 = 30/6 = 5
Σταθμισμένος Κινητός Μέσος Όρος - Περιγραφή
Σταθμίζει κάθε τιμή κλεισίματος (δεν είναι κανόνας) ανάλογα με το πόσο πρόσφατη είναι, δίνοντας στις τελευταίες μεγαλύτερη βαρύτητα και στις παλαιότερες λιγότερη.
Για τον υπολογισμό του προσθέτουμε τις τιμές κλεισίματος πολλαπλασιασμένες με την στάθμισή τους και διαιρούμε το αποτέλεσμα με το άθροισμα των σταθμίσεων.
Σταθμισμένος Κινητός Μέσος Όρος - Υπολογισμός
Για να υπολογίσουμε ένα σταθμισμένο κινητό μέσο όρο 6 ημερών των τιμών κλεισίματος μιας μετοχής, ακολουθούμε 5 απλά βήματα:
1. Αριθμούμε τις 6 τελευταίες τιμές κλεισίματος έτσι ώστε η παλαιότερη (5 ημέρες πριν) να έχει τον αριθμό 1, η προτελευταία τον αριθμό 2,...και η πιο πρόσφατη τον αριθμό 6. Οι παραπάνω αριθμοί (1,2,3,4,5,6) είναι οι σταθμίσεις μας.
2. Χρησιμοποιώντας τις παραπάνω σταθμίσεις πολλαπλασιάζουμε την τιμή κλεισίματος 5 ημέρες πριν με το 1, την τιμή κλεισίματος 4 ημέρες πριν με το 2...και την τελευταία τιμή κλεισίματος με το 6.
3. Προσθέτουμε τα γινόμενα από το βήμα 2.
4. Προσθέτουμε τις σταθμίσεις : 1+2+3+4+5+6 = 21.
5. Διαιρούμε το αποτέλεσμα του βήματος 3 με το αποτέλεσμα του βήματος 4 και καταλήγουμε στην τιμή του σταθμισμένου κινητού μέσου όρου.
Σταθμισμένος Κινητός Μέσος Όρος - Υπολογισμός
Έστω ότι μου δίνονται οι τιμές κλεισίματος των τελευταίων 6 ημερών:

Για να υπολογίσω τον σταθμισμένο μέσο όρο των τελευταίων 6 ημερών, ακολουθώ τα 5 βήματα των προηγούμενων δύο διαφανειών:
1) Οι σταθμίσεις είναι: 1,2,3,4,5,6
2) Πολλαπλασιάζω τις τιμές κλεισίματος με τις σταθμίσεις τους: 5*1=5, 3*2=6, 2*3=6, 4*4=16, 7*5=35 και 9*6=54
3) Προσθέτουμε τα γινόμενα από το βήμα 2: 5+6+6+16+35+54 = 122
4) Προσθέτουμε τις σταθμίσεις : 1+2+3+4+5+6 = 21
5) Διαιρούμε το αποτέλεσμα του βήματος 3 με το αποτέλεσμα του βήματος 4: 122/21= 5.81
Εκθετικός Κινητός Μέσος Όρος - Περιγραφή
Χρησιμοποιείται ευρέως, συνδυάζοντας με τον καλύτερο δυνατό τρόπο την "υπαιρευαισθησία" ενός σταθμισμένου κινητού μέσου όρου και την "βραδύτητα" ενός απλού κινητού μέσου όρου.
Για τον υπολογισμό του χρησιμοποιούμε την τρέχουσα τιμή κλεισίματος (δεν είναι κανόνας) και την τιμή του ΕΜΑ της προηγούμενης ημέρας (ή bar). Πιο συγκεκριμένα: ΕΜΑ = (C-EMApr.)*K+EMApr. , όπου
EMA= Exponential Moving Average.
C = Τρέχουσα τιμή κλεισίματος (δεν είναι κανόνας).
EMApr.= Η τιμή του μέσου όρου το προηγούμενο bar.
K= 2/(n+1), όπου n "the look back period".
Εκθετικός Κινητός Μέσος Όρος - Περιγραφή
ΕΜΑ = (C-EMApr.)*K+EMApr. , όπου
EMA= Exponential Moving Average.
C = Τρέχουσα τιμή κλεισίματος (δεν είναι κανόνας).
EMApr.= Η τιμή του μέσου όρου το προηγούμενο bar.
K= 2/(n+1), όπου n "the look back period".
Καθώς το n αυξάνει, το Κ μικραίνει, με αποτέλεσμα ο ΕΜΑ να γίνεται λιγότερο "ευαίσθητος" στις αλλαγές της τιμής και να προσεγγίζει τον SMA.
Όταν υπολογίζουμε για πρώτη φορά τον ΕΜΑ, ως EMApr. χρησιμοποιούμε τον SMA.
Σε αντίθεση με τους SMA & WMA, στον ΕΜΑ τα παλαιότερα δεδομένα δεν διαγράφονται από τον υπολογισμό του. Το τελευταίο έχει ως αποτέλεσμα ακόμη και αν η τιμή μείνει αμετάβλητη για n bars ο SMA & EMA να διαφέρουν στην τιμή.
Παράδειγμα
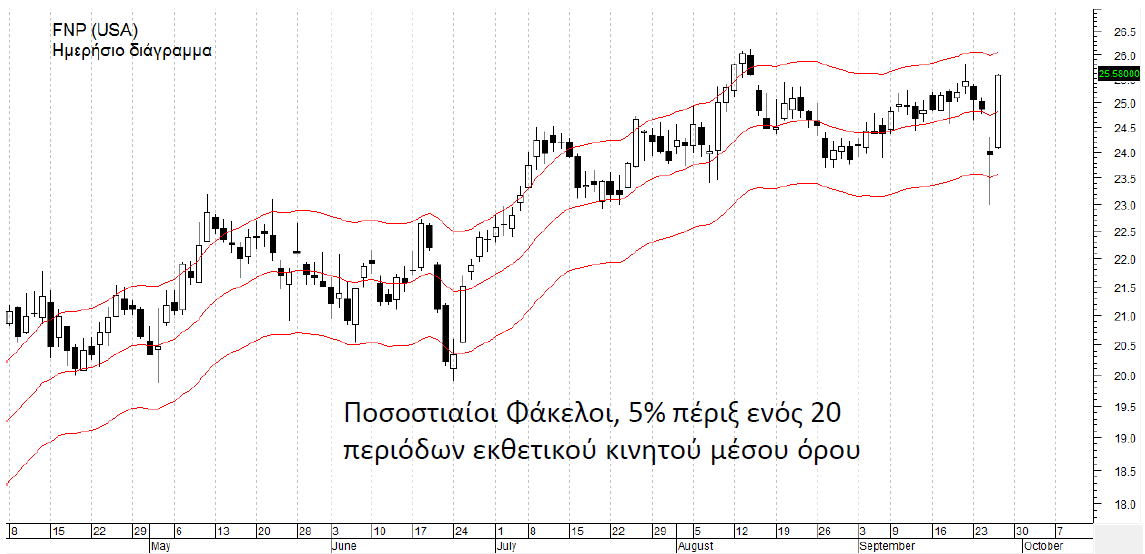
Φάκελοι (Envelopes)
Οι ποσοστιαίοι φάκελοι χρησιμοποιούνται για να μας προειδοποιήσουν πότε η τιμή έχει απομακρυνθεί αρκετά από τον κινητό μέσο όρο και έπεται (πιθανότατα) διόρθωση.
Οι φάκελοι περικλείουν τον κινητό μέσο όρο και την απόστασή τους από αυτόν την ορίζουμε εμείς σε ποσοστά (3%, 5% κ.τ.λ.). Όταν η τιμή πλησιάσει το πάνω άκρο (upper envelope), τότε η αγορά θεωρείται υπεραγορασμένη, ενώ όταν πλησιάσει στο κάτω άκρο (lower envelope) θεωρείται υπερπουλημένη.
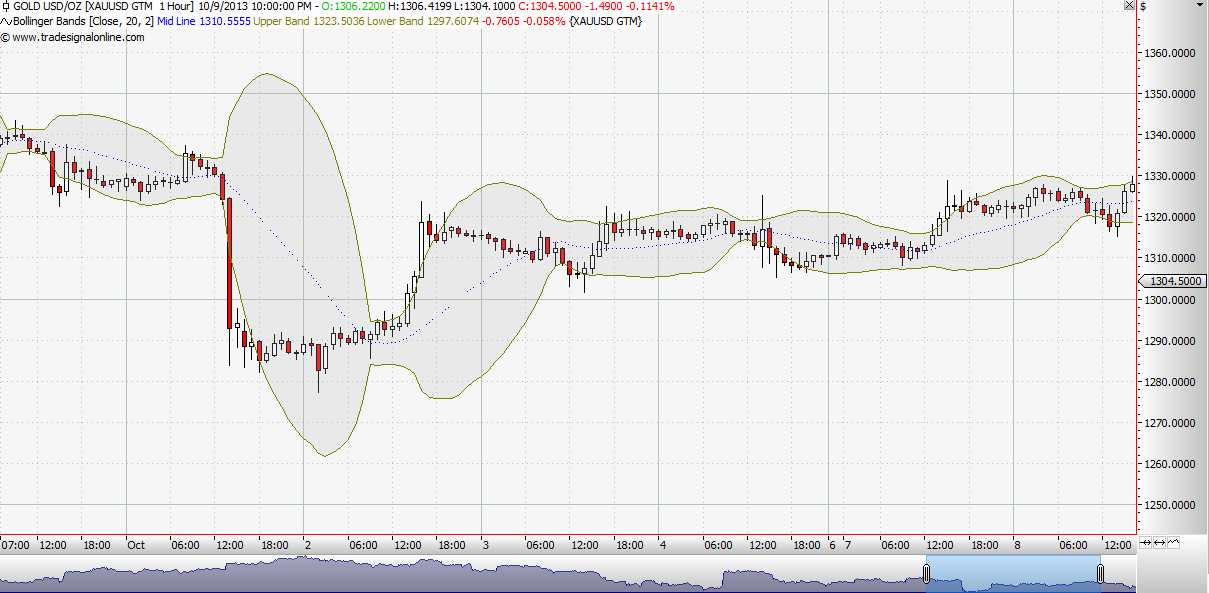
Λωρίδες Bollinger (Bollinger Bands)
Αυτή η τεχνική αναπτύχθηκε από τον John Bollinger στην δεκαετία του 1980. Όπως και οι φάκελοι, έτσι και οι λωρίδες Bollinger περιβάλλουν έναν κινητό μέσο όρο, μόνο που στα τελευταία η απόσταση μεταξύ τους δεν είναι σταθερή. Όταν η αγορά έχει αυξημένη μεταβλητότητα η απόστασή τους αυξάνεται, ενώ όταν η μεταβλητότητα είναι χαμηλή η απόσταση μικραίνει. Για να το πετύχουμε αυτό σχεδιάζουμε τις λωρίδες Bollinger, 2 τυπικές αποκλίσεις πάνω και κάτω από τον κινητό μέσο όρο. Με αυτή την τεχνική το 95% της τιμής βρίσκεται εντός των λωρίδων.
Και σε αυτή την περίπτωση όταν η τιμή πλησιάζει την άνω λωρίδα η αγορά θεωρείται υπεραγορασμένη, ενώ όταν αυτή πλησιάσει την κάτω, υπερπουλημένη.
Παρατηρήσεις
Είναι πολύ εύκολοι στην χρήση και προσαρμόζονται ανάλογα με τις απαιτήσεις του κάθε αναλυτή.
Λόγω κατασκευής, πάντα παρουσιάζουν μια καθυστέρηση (lag) στην αποτύπωση των αλλαγών της τάσης. Όσο μεγαλύτερος είναι ένας κινητός μέσος όρος, τόσο πιο αργός είναι στην αποτύπωση των αλλαγών αυτών, ενώ όσο πιο γρήγορος, τόσο πιο ευαίσθητος σε κάθε μεταβολή. Σήματα λοιπόν, εισόδου/εξόδου σε/από μία θέση δίνονται καθυστερημένα.
Τα περισσότερα άρθρα, αναλύσεις και blogs, αναφέρονται σε κινητούς μέσους όρους 20, 30, 50 και 200 ημερών.